I’ve decided that I’m going to write a sequence of blog posts to help me understand the following papers:

To do so, first we’ll get comfortable with the categories of graphs we wish to consider, then moving on to adhesive categories and then to structural decompositions.

In this post I’m going to revisit the category \(\mathsf{Grph}\) and compare it to its variant \(\mathsf{rGrph}\), which we also introduced last time. They are both categories whose objects are simple graphs, but the morphisms in \(\mathsf{Grph}\) are allowed to collapse edges into vertices. The category \(\mathsf{rGrph}\) has morphisms that don’t allow edges to be collapsed. Thus we call this the category of rigid simple graphs. In the last post we looked at how to compute some simple (co)limits in \(\mathsf{Grph}\).

In some ways I found \(\mathsf{Grph}\) a more intuitive category, but there is a pretty major big advantage to working with \(\mathsf{rGrph}\) over \(\mathsf{Grph}\). Let \(K^n\) denote the \(n\)-clique, i.e. the complete, connected graph on \((n+1)\)-vertices. Then there exists a bijection

\[\{ \text{Morphisms } f : G \to K^n \text{ in } \mathsf{rGrph} \} \cong \{ \text{$(n + 1)$-colorings of $G$} \}.\]

This isn’t true for morphisms in \(\mathsf{Grph}\) because there are always many maps \(G \to K^n\) for any graph \(G\). We can simply map all of \(G\) to any vertex of \(K^n\), as an example.

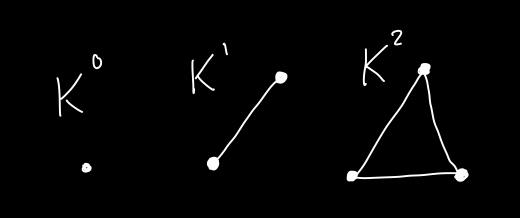
cliques

Figure 1: The first three cliques.

So in this sense, \(\mathsf{rGrph}\) is preferable, as it provides a link to the following key \(\mathbf{NP}\)-complete computational problem: Given a graph \(G\) and \(n \geq 3\), does \(G\) have an \(n\)-coloring? The theory of this computational problem ties into many areas of computer science1.

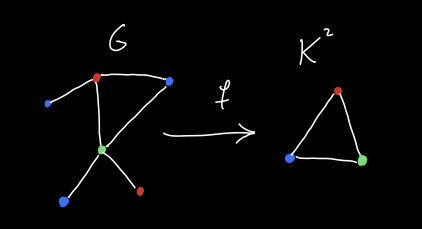
coloring

Figure 2: An example \(3\)-coloring of \(G\).

So now let us inspect \(\mathsf{rGrph}\). We know from last time that we should not expect \(\mathsf{rGrph}\) to be as nice a category as \(\mathsf{Grph}\). It is not hard to see that they have the same coproducts, but the latter category doesn’t have all pushouts (though it does have all pushouts of monomorphisms, more on this later). Now I claim that \(\mathsf{rGrph}\) and \(\mathsf{Grph}\) have the same monomorphisms, i.e. letting \(\mathsf{(r)Grph}_m\) denote the subcategory of monomorphisms, we have

\[\mathsf{Grph}_m \cong \mathsf{rGrph}_m.\]

First let us try and characterize the monomorphisms in \(\mathsf{Grph}\). Using the adjunction \(\text{Disc} \dashv V\) again, we know that \(V\) must preserve monomorphisms. In other words, if \(f: G \to H\) is a mono in \(\mathsf{Grph}\), then it cannot collapse edges. So every mono in \(\mathsf{Grph}\) is a morphism in \(\mathsf{rGrph}\).

In fact we know more than this. Because the functor \(V : \mathsf{Grph} \to \mathbf{Set}\) is faithful. Indeed, maps of graphs are completely determined by where they send vertices. Thus the functor \(V\) makes \(\mathsf{Grph}\) into a concrete category. This is also true for \(\mathsf{rGrph}\). It is well known2 that since \(V\) has a left adjoint, a morphism \(f\) in \(\mathsf{(r)Grph}\) is a monomorphism if and only if \(V(f)\) is injective.

Thus a morphism in \(\mathsf{Grph}\) is a monomorphism if and only if it is injective on vertices. But this is the same for \(\mathsf{rGrph}\). Thus they have the same monomorphisms.

In Spined Categories, they consider the categories \(\mathsf{Gr}_{hom}\), which is our \(\mathsf{rGrph}\) and \(\mathsf{Gr}_{mono}\), which is our \(\mathsf{rGrph}_m \cong \mathsf{Grph}_m\). These are also called \(\mathsf{Gr}_H\) and \(\mathsf{Gr}_M\), respectively in Structured Decompositions.

Note that if \(f : G \to H\) and \(g : G \to K\) are monomorphisms in \(\mathsf{Grph}\), then the pushout \(H +_G K\) exists in \(\mathsf{Grph}\) as we showed last time, and it is not too hard to show that it also exists in \(\mathsf{rGrph}\)3. However, this pushout might not exist in \(\mathsf{rGrph}_m\). Indeed, consider the following pushout.

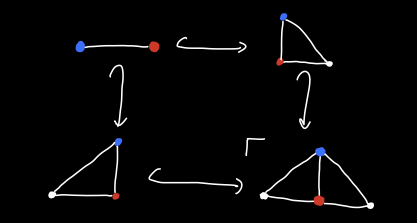
pushout

Figure 4: Example of a pushout in \(\mathsf{rGrph}\)

Now there is a commutative diagram in \(\mathsf{rGrph}\) as follows:

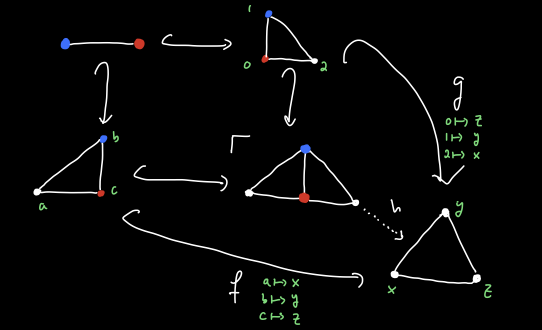
induced map from pushout

Figure 4: Induced map from pushout.

Which induces a unique map \(h\). Now \(h\) cannot be a monomorphism, simply because there are more vertices in the domain than in the codomain. In other words, we’ve constructed a cocone in \(\mathsf{rGrph}_m\) and the colimit in \(\mathsf{rGrph}\) does not map to it by a monomorphism. Using this idea, we can show that not all pushouts exist in \(\mathsf{rGrph}_m \cong \mathsf{Grph}_m\).

However the important thing to note is that pushouts along monomorphisms exist in \(\mathsf{rGrph}\), though the resulting induced map may not itself be a monomorphism. We’ll dive more deeply into this property in the next post on adhesive categories.

  1. Such as those given here. ↩

  2. See here for proofs. ↩

  3. Just consider the description of the pushout in \(\mathsf{Grph}\) and notice that none of the maps involve collapsing edges. ↩